Nach 5 Jahren wurde jetzt die DIN EN ISO 18314-2, Analytische Farbmessung — Teil 2: Saunderson‑Korrektur, Lösungen der Kubelka‑Munk‑Gleichung, Farbstärke, Farbtiefe und Deckvermögen, überarbeitet. Dabei wurde der Titel um „Farbtiefe“ ergänzt und die Begriffe im Abschnitt 3 wurden an ISO 18451-1, Pigmente, Farbstoffe und Füllstoffe — Begriffe — Teil 1: Allgemeine Begriffe, angeglichen. Die Norm ist mit Ausgabe Februar 2023 veröffentlicht.

DIN EN ISO 18314-2 legt die Saunderson Korrektur für unterschiedliche Messgeometrien sowie die Lösungen der Kubelka Munk Gleichung für deckende und durchsichtige Schichten fest. Sie legt außerdem Verfahren zur Berechnung der Farbstärke, einschließlich des Restfarbabstandes, mit unterschiedlichen Kriterien, die auf der Farbtiefe beruhen, fest. Schließlich werden Verfahren zur Bestimmung des Deckvermögens zur Verfügung gestellt.

Saunderson Korrektur

Bei farbmetrischen Berechnungen ist es notwendig, Oberflächenphänomene zu berücksichtigen, um brauchbare Ergebnisse zu erhalten. Die Gleichungen sind als Saunderson-Korrektur bekannt. Die notwendigen Koeffizienten sind Lösungen der Fresnel Gleichungen in Abhängigkeit von der Brechzahl des gegebenen Bindemittels.

Die Formeln sind abgeleitet unter der Annahme optimaler Oberflächen, einer perfekt deckenden Schicht und einer perfekten diffusen Lichtstreuung im Inneren der Probe. Jede Abweichung von diesen Annahmen muss Abwägungen der Zweckmäßigkeit der folgenden Berechnungen zur Folge haben.

Die in DIN EN ISO 18314-2 angegebenen Gleichungen gelten für zwei der am weitesten verbreiteten Geometrien: diffuse Beleuchtung, 0° Beobachtung (d:0°) und 45° Einfallwinkel, 0° Beobachtung (45°:0°). In nahezu jedem verwendeten Farbmessgerät ist der verwendete Beobachtungswinkel nicht 0°, sondern 8°. Diese Abweichung wird als unproblematisch eingeschätzt.

Lösung der Kubelka Munk Gleichungen

Die Kubelka Munk Theorie beschreibt die Reflexion einer pigmentierten Beschichtung durch zwei Konstanten: Absorption, K(λ), und Streuung, S(λ). Sie geht von den folgenden Annahmen aus:

            a) ideal diffuse Strahlungsverteilung auf der Beleuchtungsseite;

            b) ideal diffuse Strahlungsverteilung im Inneren der Schicht;

            c) keine Beachtung von Oberflächenphänomenen, die aus der Diskontinuität der

Brechzahl resultieren.

Für eine unendlich dicke bzw. deckende Schicht mit einem Reflexionsfaktor von 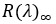  finden sich die in den folgenden Gleichungen gezeigten Lösungen, die die Bestimmung der Beziehung zwischen dem Streu  und dem Absorptionskoeffizienten erlauben:

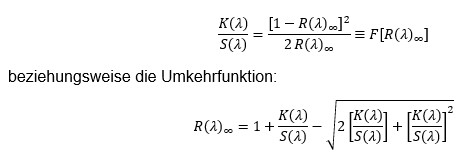
Für die Bestimmung des Streu und des Absorptionskoeffizienten können zwei unterschiedliche Verfahren angewendet werden (es muss die Saunderson Korrektur verwendet werden).

Bestimmung der relativen Farbstärke und des Restfarbabstandes von Buntpigmenten

Alle in DIN EN ISO 18314-2 festgelegten Verfahren setzen, zumindest näherungsweise, eine lineare Beziehung zwischen der Farbmittelkonzentration und der Kubelka Munk Funktion voraus.

Es wird angenommen, dass die gemessene Streuung der Beschichtungen vom Weißpigment und die Absorption vom Buntpigment dominiert wird. All diese Bedingungen müssen erfüllt werden, um korrekte Ergebnisse der in DIN EN ISO 183142 beschriebenen Verfahren zu ermitteln. Die Kubelka Munk Funktion für die Weißpaste kann in den meisten Fällen vernachlässigt werden.

Bestimmung des Deckvermögens pigmentierter Medien

Der Deckvermögenswert kennzeichnet, welche Fläche, in Quadratmeter, eines gegebenen Kontrastsubstrates mit der Mengeneinheit der Probe so beschichtet werden kann, dass eine festgelegte Deckvermögenskenngröße erreicht wird. Die Deckvermögenskenngröße muss ein vereinbarter Farbabstand zwischen den beiden kontrastierenden Flächen des beschichteten Kontrastsubstrates sein. ΔE_"ab" ^*=1 wird üblicherweise angewendet.  Für achromatische Beschichtungen wird ein Kontrastverhältnis von 0,98 verwendet, um den 2 Prozent Schwellenwert für die Helligkeitsempfindung des menschlichen Auges zu berücksichtigen. Werte des Reflexionsfaktors von nahe Null für schwarze und 0,8 für weiße Substrate werden verwendet. 

Der durch alle Verfahren bestimmte Parameter ist die geringste Schichtdicke hD, die notwendig ist, um die verwendeten Kenngrößen zu erfüllen. Der Kehrwert dieses Parameters ist das Äquivalent zum Deckvermögenswert D = 1/hD. Der Deckvermögenswert kann auf folgende Weisen bestimmt und festgelegt werden:

            - Deckvermögenswert Dv, in Quadratmeter je Liter;

            - Deckvermögenswert Dm, in Quadratmeter je Kilogramm.

Dv und Dm kennzeichnen jeweils die Fläche des betreffenden Kontrastsubstrates, in Quadratmetern, die mit 1 l oder 1 kg des pigmentierten Mediums deckend (im Sinne der Deckvermögenskenngröße) beschichtet werden kann.

Farbmetrische Verfahren zur Bestimmung des Deckvermögens verwenden die allgemeinen Lösungen der Kubelka Munk Gleichung in Verbindung mit einem Iterationsverfahren zur Bestimmung der notwendigen Schichtdicke, die die gewählten Deckvermögenskenngrößen erfüllt. Dies ist der direkteste Weg, der zu den besten Ergebnissen führt.

Es ist möglich, mit zwei nichtdeckenden Schichten auf weißen und schwarzen Substraten oder mit einer deckenden Schicht in Verbindung mit einer nichtdeckenden Schicht auf einem schwarzen oder weißen Substrat zu arbeiten. Das Verfahren sollte vorzugsweise durch die Überprüfung der verfügbaren Daten bestimmt werden.